Description
Algorithm: Generate an arithmetic checksum tree for a Bitcoin private key.
Contents
- Description
- Contents
- Bitcoin Private Key Formats
- Hexadecimal Addition
- Algorithm: Generate an arithmetic checksum tree for a Bitcoin private key.
- Worked Example
Bitcoin Private Key Formats
Example Bitcoin private key (64 characters, 32 bytes):
7972b641101c0ad67b0e401b800a9b6f3225c97fc6b8115042cf66968c2fb2e5
The corresponding Bitcoin address is:
16ASCUS3s7D4UQh6J9oHGuT19agPvD3PFj
It's easier to read the private key if it is written in a grid pattern, divided into groups of 4 characters and lines of 4 groups.
Here is the example private key in this grid format. I call this a "grid key".
7972 b641 101c 0ad6
7b0e 401b 800a 9b6f
3225 c97f c6b8 1150
42cf 6696 8c2f b2e5
7b0e 401b 800a 9b6f
3225 c97f c6b8 1150
42cf 6696 8c2f b2e5
A few errors in the private key can make it impossible to recover the actual private key within a reasonable time frame. I therefore prefer to generate an arithmetic checksum tree for the private key in order to make it more robust - errors can be located more precisely, and key recovery time is drastically improved.
Note: I originally developed this approach in the project An investigation into recovering from transcription errors in Bitcoin private keys. More detail is available there.
Here is the example private key, in grid format with the added arithmetic checksum tree. I call this a "storage key".
9
ab31
96ed 0029 cb57 1b50
7972 b641 101c 0ad6
7b0e 401b 800a 9b6f
3225 c97f c6b8 1150
42cf 6696 8c2f b2e5
ab31
96ed 0029 cb57 1b50
7972 b641 101c 0ad6
7b0e 401b 800a 9b6f
3225 c97f c6b8 1150
42cf 6696 8c2f b2e5
The checksum values are produced by hexadecimal addition. The primary reason for doing this instead of using a hash checksum is that, if necessary, the checksum tree can calculated manually using pencil, paper, and a hexadecimal addition table. Note: The table itself could be generated manually with pencil and paper.
Hexadecimal Addition
Standard human numbers are base 10 and the digits are:
0, 1, 2, 3, 4, 5, 6, 7, 8, 9
Hex numbers are base 16 and the digits are:
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, a, b, c, d, e, f
Hexadecimal addition works in the same way as standard base 10 addition, but in base 16. Some examples:
0 + 0 = 0
0 + 1 = 1
1 + 1 = 2
1 + 9 = a
1 + a = b
5 + a = f
6 + a = 10
1 + f = 10
f + a = 19
f + e = 1d
f + f = 1e
1f + 1 = 20
0 + 1 = 1
1 + 1 = 2
1 + 9 = a
1 + a = b
5 + a = f
6 + a = 10
1 + f = 10
f + a = 19
f + e = 1d
f + f = 1e
1f + 1 = 20
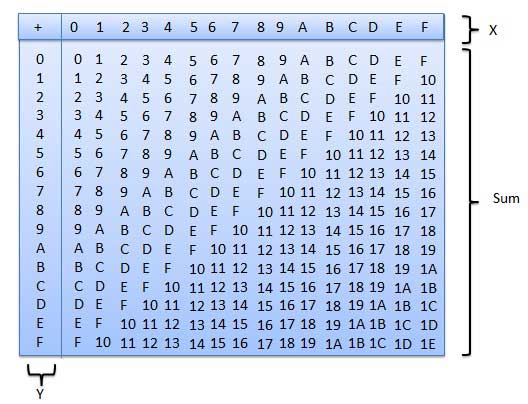
This hexadecimal addition table [0] shows all the possible results for adding two single-digit hex numbers:
Description of hexadecimal addition table: Two axes, X and Y. X runs horizontally along the top of the table. Y runs vertically down the left side of the table. Both X and Y contain the hex values 0-f. Each entry in the table is the hex sum of the relevant X and Y values. Examples: 0 + 0 = 0, f + f = 1e.
Algorithm: Generate an arithmetic checksum tree for a Bitcoin private key.
-) Take a Bitcoin private key and convert it into grid format.
-) Arithmetic checksum function: For a group of 4 characters, treat each character as a hex number, sum the characters, and take the last character of the resulting hex number.
-) Calculate the arithmetic checksum of each group in the first line of the private key. This will produce 4 checksum characters. Write this new group on a new line above the key.
-) Do the previous step for the remaining 3 lines in the private key, writing each new group on the same new line above the key. Result: A single new "checksum line" of 4 groups.
-) Apply the same technique to the checksum line itself. Calculate the arithmetic checksum of each of its 4 groups. This will produce a single "checksum group" of 4 characters. Write this on a new line above the checksum line.
-) Apply the same technique to the checksum group. Calculate the arithmetic checksum of the single checksum group. This will produce a single "checksum character". Write this on a new line above the checksum group.
Notes:
- I use this format when writing a Bitcoin private key on paper
- I have developed tools that rely on this algorithm to convert a private key to and from the checksum tree storage format:
Tools for storing a Bitcoin private key with a checksum tree
Worked Example
Bitcoin private key:
7972b641101c0ad67b0e401b800a9b6f3225c97fc6b8115042cf66968c2fb2e5
Convert to grid format:
7972 b641 101c 0ad6
7b0e 401b 800a 9b6f
3225 c97f c6b8 1150
42cf 6696 8c2f b2e5
7b0e 401b 800a 9b6f
3225 c97f c6b8 1150
42cf 6696 8c2f b2e5
Calculate the arithmetic checksum of group 1 in line 1:
group: 7972
- Treating each character as a hex number, sum the numbers:
7 + 9 = 10
10 + 7 = 17
17 + 2 = 19
- Take the last character of the resulting hex number:
9
- Treating each character as a hex number, sum the numbers:
7 + 9 = 10
10 + 7 = 17
17 + 2 = 19
- Take the last character of the resulting hex number:
9
Calculate the arithmetic checksum of group 2 in line 1:
group: b641
b + 6 = 11
11 + 4 = 15
15 + 1 = 16
last character: 6
b + 6 = 11
11 + 4 = 15
15 + 1 = 16
last character: 6
Calculate the arithmetic checksums of groups 3 and 4 in line 1:
group: 101c
- checksum: e
group: 0ad6
- checksum: d
- checksum: e
group: 0ad6
- checksum: d
The first group in the checksum line is therefore:
96ed
This first group corresponds to the first line of the private key.
Calculate the rest of the checksum line in the same way. Result:
96ed 0029 cb57 1b50
Group 2 in the checksum line corresponds to line 2 of the private key. Group 3 corresponds to line 3, and group 4 to line 4.
Let's add the checksum line above the private key:
96ed 0029 cb57 1b50
7972 b641 101c 0ad6
7b0e 401b 800a 9b6f
3225 c97f c6b8 1150
42cf 6696 8c2f b2e5
7972 b641 101c 0ad6
7b0e 401b 800a 9b6f
3225 c97f c6b8 1150
42cf 6696 8c2f b2e5
Now, calculate the checksum group from the checksum line.
group: 96ed
9 + 6 = f
f + e = 1d
1d + d = 2a
last character: a
group: 0029
0 + 0 + 2 = 2
2 + 9 = b
last character: b
group: cb57
c + b = 17
17 + 5 = 1c
1c + 7 = 10 + c + 7 = 10 + 13 = 23
last character: 3
group: 1b50
1 + b = c
c + 5 = 11
11 + 0 = 11
last character: 1
9 + 6 = f
f + e = 1d
1d + d = 2a
last character: a
group: 0029
0 + 0 + 2 = 2
2 + 9 = b
last character: b
group: cb57
c + b = 17
17 + 5 = 1c
1c + 7 = 10 + c + 7 = 10 + 13 = 23
last character: 3
group: 1b50
1 + b = c
c + 5 = 11
11 + 0 = 11
last character: 1
So, now we have the checksum group:
ab31
Let's add it above the checksum line:
ab31
96ed 0029 cb57 1b50
7972 b641 101c 0ad6
7b0e 401b 800a 9b6f
3225 c97f c6b8 1150
42cf 6696 8c2f b2e5
96ed 0029 cb57 1b50
7972 b641 101c 0ad6
7b0e 401b 800a 9b6f
3225 c97f c6b8 1150
42cf 6696 8c2f b2e5
Calculate the arithmetic checksum of the checksum group:
a + b = 15
15 + 3 = 18
18 + 1 = 19
last character: 9
15 + 3 = 18
18 + 1 = 19
last character: 9
The checksum character of the entire private key is:
9
The final storage key is therefore:
9
ab31
96ed 0029 cb57 1b50
7972 b641 101c 0ad6
7b0e 401b 800a 9b6f
3225 c97f c6b8 1150
42cf 6696 8c2f b2e5
ab31
96ed 0029 cb57 1b50
7972 b641 101c 0ad6
7b0e 401b 800a 9b6f
3225 c97f c6b8 1150
42cf 6696 8c2f b2e5